递归

例题

LeetCode70

假设你正在爬楼梯。需要 n 阶你才能到达楼顶。

每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢？

示例1

输入：n = 2
输出：2
解释：有两种方法可以爬到楼顶。

1. 1 阶 + 1 阶
2. 2 阶

示例2

输入：n = 3
输出：3
解释：有三种方法可以爬到楼顶。

1. 1 阶 + 1 阶 + 1 阶
2. 1 阶 + 2 阶
3. 2 阶 + 1 阶

提示

1 <= n <= 45

解题思想

可以令 f(n) 为走到第 n 层楼梯的走法数量
由于一步可以走一层或两层，所以一步走到第 n 层楼梯的层次为 n-1 和 n-2 层
此时如果知道 f(n-1) 和 f(n-2)，则可以计算 f(n) = f(n-1) + f(n-2)
则可以有已知的 f(1) = 1 和 f(2) = 2 往后递归出 f(n)

示例代码

public class Solution {
    public int climbStairs(int n) {
        int[] nums = new int[3];
        // 分别存储 n-2 、 n-1 和 n 层台阶的走法
        nums[0] = 1;
        nums[1] = 1;
        nums[2] = 1;
        for (int i=1; i<n; i++) {
            nums[2] = nums[0] + nums[1];
            // n 层台阶的走法数量为 n-2层 + n-1层的走法数量
            nums[0] = nums[1];
            // 此时 n-2 层更新为原来的 n-1 层
            nums[1] = nums[2];
            // 此时 n-1 层更新为原来的 n 层
        }
        return nums[2];
        // 返回结果
    }
}

---

LeetCode112

给你二叉树的根节点 root 和一个表示目标和的整数 targetSum 。判断该树中是否存在根节点到叶子节点的路径，这条路径上所有节点值相加等于目标和 targetSum 。如果存在，返回 true ；否则，返回 false 。

注：叶子节点 是指没有子节点的节点。

示例1

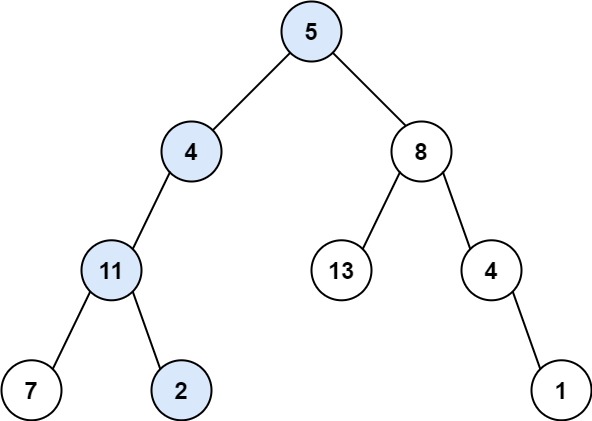
输入：root = [5,4,8,11,null,13,4,7,2,null,null,null,1], targetSum = 22
输出：true
解释：等于目标和的根节点到叶节点路径如上图所示。

示例2

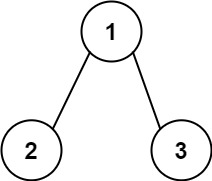
输入：root = [1,2,3], targetSum = 5
输出：false
解释：树中存在两条根节点到叶子节点的路径：
(1 --> 2): 和为 3
(1 --> 3): 和为 4
不存在 sum = 5 的根节点到叶子节点的路径。

示例3

输入：root = [], targetSum = 0
输出：false
解释：由于树是空的，所以不存在根节点到叶子节点的路径。

提示

树中节点的数目在范围 [0, 5000] 内
-1000 <= Node.val <= 1000
-1000 <= targetSum <= 1000

解题思想

直接后序遍历整颗树到叶子节点
即逐层递归，直到左右子节点均为null
当递归到子节点时，判断累加的值和目前节点的值相加是否为目标值即可

示例代码

public boolean hasPathSum(TreeNode root, int targetSum) {
    return dfs(root, targetSum, 0);
    // 返回递归结果
}

public static boolean dfs (TreeNode p, int targetSum, int now) {
    // 递归
    if (p == null) return false;
    // 如果此结点为空，则返回false
    if ((now + p.val) == targetSum && p.left == null && p.right == null) {
        // 目前的值 + 当前节点的值为目标值 且 该结点为叶子结点 则返回true
        return true;
    }
    boolean left = left = dfs(p.left, targetSum, now+p.val);
    boolean right = dfs(p.right, targetSum, now+p.val);
    // 分别递归左右子节点
    return left || right;
    // 只要左右子节点有一个是对的，就返回true，否则返回false
}

LeetCode509

与 LeetCode70 一样